Primera Ley de la Termodinamica

Instituto de Tecnología Universitario Antonio Jose de Sucre

Ampliación Guarenas

3 Semestre Mecánica

Materia: Termodinámica

Profesora: ing. Ranielina Rondón

Alumno: Francisco Jose Liendo Berroteran 

_________________________________________________________________________________

Primera Ley de la Termodinámica: determina que la energía interna de un sistema aumenta cuando se le transfiere calor o se realiza un trabajo sobre él. Su expresión depende del criterio de signos para sistemas termodinámicos elegido:

Criterio IUPAC 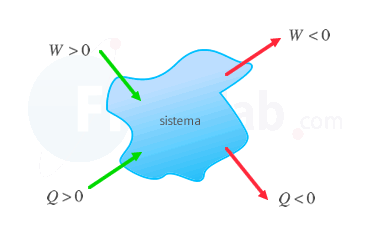Se considera positivo aquello que aumenta la energía interna del sistema, o lo que es lo mismo, el trabajo recibido o el calor absorbido. Criterio tradicional 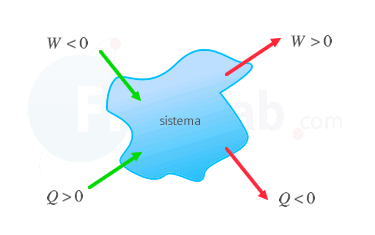Se considera positivo el calor absorbido y el trabajo que realiza el sistema sobre el entorno. ΔU=Q+W ΔU=Q−W

Donde:
∆U : Incremento de energía interna del sistema ( ∆U = Ufinal - Uinicial ). Su unidad de medida en el Sistema Internacional es el julio ( J )
Q : Calor intercambiado por el sistema con el entorno. Su unidad de medida en el Sistema Internacional es el julio ( J ), aunque también se suele usar la caloría ( cal ). 1 cal = 4.184 J
W : Trabajo intercambiado por el sistema con el entorno. Su unidad de medida en el Sistema Internacional es el julio ( J )

Al igual que todos los principios de la termodinámica, el primer principio se basa en sistemas en equilibrio.

Por otro lado, es probable que hayas oído más de una vez que la energía ni se crea ni se destruye, solo se transforma. Se trata del principio general de conservación de la energía. Pues bien, la primera ley de la termodinámica es la aplicación a procesos térmicos de este principio. En un sistema aislado, en el que no se intercambia energía con el exterior, nos queda:


ΔU=0



El universo en su totalidad se podría considerar un sistema aislado, y por tanto, su energía total permanece constante.

Finalmente observa que, al ser una función de estado, la diferencia de energía interna solo depende de los estados inicial y final, ∆U = Uf - Ui , y no del camino que haya seguido el proceso. El calor y el trabajo, en cambio, no son funciones de estado, por lo que sus valores dependen del camino seguido por el proceso. Esto quedará bien ilustrado en los diagramas presión - volumen para gases ideales, como verás más abajo.

Ejercicios

1.- ¿Cuál es el incremento en la energía interna de un sistema si se le suministran 700 calorías de calor y se le aplica un trabajo de 900 Joules?

Solución: El problema indica que se le están suministrando 700 calorías de calor, eso quiere decir que  será positivo, por otra parte nos dice que al sistema se le aplicará un trabajo de 900 Joules, aquí el signo de  tendrá que ser negativo, puesto que se la están aplicando al sistema.

Sabiendo ese análisis podemos dar solución al problema de la siguiente forma:

Vamos a convertir las 700 calorías de calor en Joules. ¿Por qué? Porque el S.I (Sistema Internacional) de medida así lo estandariza.

Recordar que  porque como dijimos, al sistema se le está aplicando un trabajo. Ahora conforme a la fórmula de la primera ley de la termodinámica, iniciemos a sustituir.

despejando ” “

Sustituyendo

Ese sería el resultado de nuestro incremento en la energía interna.

_________________________________________________________________________________

2.- Suponga que un sistema pasa de un estado a otro, intercambiando energía con su vecindad. Calcule la variación de energía interna del sistema en los siguientes casos:

a) El sistema absorbe 100 cal y realiza un trabajo de 200 J.

b) El sistema absorbe 100 cal y sobre él se realiza un trabajo de 200 J.

c) El sistema libera 100 cal de calor a la vencidad (alrededor), y sobre él se realiza un trabajo de 200 J.

##

a) Para iniciar a resolver este inciso, debemos entender lo que nos pide.

+ El sistema absorbe 100 cal , que convertiremos en Joules.

+ El sistema realiza el trabajo de 200 J.

Convertimos lo que que absorbe el sistema:

Ahora esto nos indica que por fórmula tendremos:

Observamos que la energía interna del sistema aumenta considerablemente a 218 J.

b) Para este caso analizamos de la siguiente manera el inciso.

+ El sistema absorbe 100 cal

– El trabajo fue realizado sobre el sistema 200J

Por fórmula tenemos:

Por lo que ahora, tenemos 618 Joules, y observamos un gran incremento de la energía interna.

Y finalmente el último inciso.

c) En este caso el sistema hace las dos versiones distintas al inciso a), pues aquí tenemos el siguiente análisis.

– El sistema libera 100 cal [Se convierte a Joules]

– Se le aplica un trabajo sobre el sistema de 200 J

Por fórmula tendríamos algo así:

Vemos que la energía del sistema disminuye considerablemente, y esto es lógico puesto que nada más recibió 200 J de energía y a su vez estaba liberando 418 Joules.